图论入门(完结)-程序员宅基地
更新线
- 图的基本概念(已更)
- 图的存储结构(邻接矩阵、邻接表、链式前向星)(已更)
- 图的遍历(深度优先、广度优先)(已更)
- 一笔画问题(欧拉回路,已更)
- 哈密顿路问题(已更)
- 最短路径(已更)
- 最小生成树(已更)
图论简介及相关概念
图 ( g r a p h ) (graph) (graph) 是一个二元组 G = ( V ( G ) , E ( G ) ) G=(V(G),E(G)) G=(V(G),E(G)),其中 V ( G ) V(G) V(G)是非空集,称为点集 ( v e r t e x s e t ) (vertex set) (vertexset),对于 V V V中的每个元素,我们称其为顶点 ( v e r t e x ) (vertex) (vertex)或节点 ( n o d e ) (node) (node),简称点, E ( G ) E(G) E(G)为 V ( G ) V(G) V(G)各结点之间边的集合,称为边集 ( e d g e s e t ) (edge set) (edgeset)
常用 G = ( V , E ) G=(V,E) G=(V,E) 表示图
- 当 V , E V,E V,E都是有限集合时,称 G G G为有限图
- 当 V V V或 E E E都是有限集合时,称 G G G为无限图
图有多种,包括无向图 ( u n d i r e c t e d g r a p h ) (undirected graph) (undirectedgraph),有向图 ( d i r e c t e d g r a p h ) (directed graph) (directedgraph),混合图 ( m i x e d g r a p h ) (mixed graph) (mixedgraph),带权图 等
举个例子

无向图专业术语
- 两个顶点之间如果有边连接,那么就视为两个顶点相邻
- 路径:相邻顶点的序列
- 圈:起点和终点重合的路径
- 连通图:任意两点之间都有路径连接的图
- 度:顶点连接的边数叫做这个顶点的度
- 树:没有圈的连通图
- 森林:没有圈的非连通图
有向图专业术语
- 在有向图中,边是单向的:每条边所连接的两个顶点是一个有序对,他们的邻接性是单向的
- 有向路径:相邻顶点的序列
- 有向环:一条至少含有一条边且起点和终点相同的有向路径
- 有向无环图 ( D A G ) (DAG) (DAG):没有环的有向图
- 度:一个顶点的入度与出度之和称为该顶点的度
1 ) ) ).入度:以顶点为弧头的边的数目称为该顶点的入度
2 ) ) ).出度:以顶点为弧尾的边的数目称为该顶点的出度
图的存储方式
1.邻接矩阵
方法:对于一个有 V V V的顶点的图而言,可以使用 V ∗ V V*V V∗V的二维数组表示 G [ i ] [ j ] G[i][j] G[i][j]表示的是顶点 i i i与顶点 j j j的关系。如果顶点 i i i和顶点 j j j之间有边相连, G [ i ] [ j ] = 1 G[i][j]=1 G[i][j]=1如果顶点 i i i和顶点 j j j之间无边相连, G [ i ] [ j ] = 0 G[i][j]=0 G[i][j]=0,对于无向图: G [ i ] [ j ] = G [ j ] [ i ] G[i][j]=G[j][i] G[i][j]=G[j][i]

代码实现:
bool adj[MAXN][MAXN];
scanf("%d %d", &n , &m);
for (int i = 1 ; i <= m ; i ++) {
int u , v;
scanf("%d %d", &u , &v);
adj[u][v] = 1;
adj[v][u] = 1;
}
2.邻接表
方法:使用一个支持动态增加元素的数据结构构成的数组,如 v e c t o r vector vector< i n t int int> a d j [ n + 1 ] adj[n + 1] adj[n+1] 来存边,其中 a d j [ u ] adj[u] adj[u]存储的是点的所有出边的相关信息 ( ( (终点、边权等 ) ) )
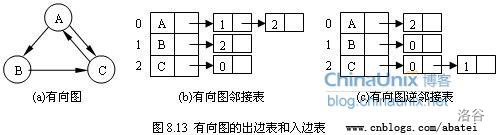
代码实现:
struct node{
vector<int> v;
}a[MAXN];
for (int i = 1 ; i <= m ; i ++) {
int u , v;
scanf("%d %d", &u , &v);
a[u].v.push_back(v);
a[v].v.push_back(u);
}
return 0;
3.链式前向星
方法:
对于这样一张有向图:
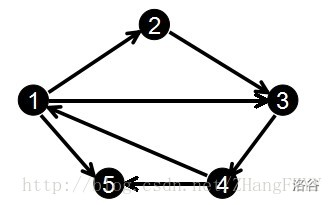
输入边的顺序如下:
1 2
2 3
3 4
1 3
4 1
1 5
4 5
对于邻接表来说是这样的:
1 -> 2 -> 3 -> 5
2 -> 3
3 -> 4
4 -> 1 -> 5
5 -> ^
对于链式前向星来说是这样的:
edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;
简化后:1 -> 5 -> 3 -> 2
核心代码:
struct edge{
int to , nxt , w;
};
edge a[MAXN];
void add(int u , int v , int w) {
a[cnt].w = w;
a[cnt].to = v;
a[cnt].nxt = head[u];
head[u] = cnt ++;
}
图的遍历
(内置芝士)什么是图的遍历:从图中的某个顶点出发,按某种方法对图中的所有顶点访问且仅访问一次。为了保证图中的顶点在遍历过程中仅访问一次,要为每一个顶点设置一个访问标志
1.有向图的dfs
题目大意:
给定一个有向图,有 N N N个顶点, M M M条边,顶点从 1.. N 1..N 1..N依次编号,求出字典序最小的深度优先搜索顺序
总体思路:
利用邻接表存储点的关系,将点放入 d f s dfs dfs里搜索与之相邻但未被遍历过的点
核心代码如下:
void dfs(int k) {
if (vis[k]) return;
vis[k] = 1;
printf("%d ", k);
for (set<int>:: iterator it = st[k].begin() ; it != st[k].end() ; it ++) {
dfs(*it);
}
}
for (int i = 1 ; i <= m ; i ++) {
int u , v;
scanf("%d %d", &u , &v);
st[u].insert(v);
}
dfs(1);
for (int i = 1 ; i <= n ; i ++) {
if (!vis[i]) dfs(i);
}
2.有向图的bfs
题目大意:
给定一个有向图,有 N N N个顶点, M M M条边,顶点从 1 1 1… N N N依次编号,求出字典序最小的宽度优先搜索顺序
思路:
利用邻接表存储点的关系,将点放入 b f s bfs bfs里搜索与之相邻但未被遍历过的点
核心代码如下:
void bfs(int k) {
q.push(k);
while(!q.empty()) {
int x = q.front();
q.pop();
if (vis[x]) continue;
vis[x] = 1;
printf("%d ", x);
for (set<int>:: iterator it = st[x].begin() ; it != st[x].end() ; it ++) {
q.push(*it);
}
}
}
for (int i = 1 ; i <= m ; i ++) {
int u , v;
scanf("%d %d", &u , &v);
st[u].insert(v);
}
bfs(1);
for (int i = 1 ; i <= n ; i ++) {
if (!vis[i]) bfs(i);
}
3.无向图的bfs
题目大意:
一个无向图,从指定顶点出发进行 B F S BFS BFS,求遍历得到的顶点序
总体思路:
利用邻接矩阵存储边(每一层要从小到大排序,矩阵方便操作),将点放入 b f s bfs bfs里搜索与之相邻但未被遍历过的点
核心代码如下:
void bfs() {
q.push(rt);
while(!q.empty()) {
int x = q.front();
q.pop();
if (vis[x]) continue;
vis[x] = 1;
printf("%d ", x);
for (int i = 1 ; i <= n ; i ++) {
if (adj[x][i]) {
q.push(i);
}
}
}
}
for (int i = 1 ; i <= m ; i ++) {
int u , v;
scanf("%d %d", &u , &v);
adj[u][v] = 1;
adj[v][u] = 1;
}
一笔画问题(欧拉路)
Ps:欧拉路指的是:存在这样一种图,可以从其中一点出发,不重复地走完其所有的边如果欧拉路的起点与终点相同,则称之为欧拉回路
需满足条件:
- 图是连通的,若不连通不可能一次性遍历所有边
- 对于无向图:有且仅有两个点,与其相连的边数为奇数,其他点相连边数皆为偶数;或所有点皆为偶数边点。对于两个奇数点,一个为起点,一个为终点。起点需要出去,终点需要进入,故其必然与奇数个边相连
- 如果存在这样一个欧拉路,其所有的点相连边数都为偶数,那说明它是欧拉回路
- 对于有向图:除去起点和终点,所有点的出度与入度相等。起点出度比入度大1,终点入度比出度大1。若起点终点出入度也相同,则为欧拉回路
利用 d f s dfs dfs求一笔画路径
题目大意:
根据一笔画的两个定理,如果寻找欧拉回路,对任意一个点执行深度优先遍历;找欧拉路,则对一个奇点执行 d f s dfs dfs,时间复杂度为 O ( m + n ) O(m+n) O(m+n), m m m为边数, n n n是点数
总体思路:
即把奇点作为起点放入 d f s dfs dfs搜索,每搜索到一个相邻的点即把这条边删掉,若所有边都遍历到了,输出答案
核心代码如下:
void dfs(int k , int id) {
ans[id] = k;
bool f = 1;
for (int i = 1 ; i <= n ; i ++) {
for (int j = 1 ; j <= m ; j ++) {
if (a[i][j]) {
f = 0;
break;
}
}
}
if (f) {
for (int i = 1 ; i <= id ; i ++) {
printf("%d ", ans[i]);
}
exit(0);
}
for (int i = 1 ; i <= n ; i ++) {
if (a[k][i]) {
a[k][i] = 0;
a[i][k] = 0;
dfs(i , id + 1);
a[k][i] = 1;
a[i][k] = 1;
}
}
}
d f s dfs dfs暴力求解哈密顿图
思路:利用邻接表存储边的关系,枚举1~ n n n作为起点的情况,然后每搜到一种情况便把 a n s ans ans加 1 1 1即可
int dfs(int k , int cnt) {
if(cnt == n) return 1;
int res = 0;
for (int i = 1 ; i <= h[k][0] ; i ++) {
if (!vis[h[k][i]]) {
vis[h[k][i]] = 1;
res += dfs(h[k][i] , cnt + 1);
vis[h[k][i]] = 0;
}
}
return res;
}
for (int i = 1 ; i <= n ; i ++) {
vis[i] = 1;
ans += dfs(i , 1);
vis[i] = 0;
}
最短路问题
最短路径问题是图论研究中的一个经典算法问题, 旨在寻找图 ( ( (由结点和路径组成的 ) ) )中两结点之间的最短路径。
例如:
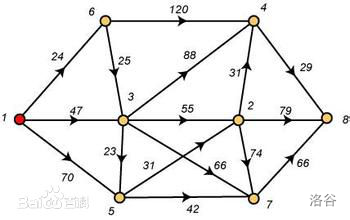
1. f l o y d floyd floyd
佛洛伊德是最简单的最短路径算法,可以计算图中任意两点间的最短路径。时间复杂度为 O ( N 3 ) O(N^3) O(N3),适用于出现负边权的情况
算法描述:
- 初始化:
点 u u u、 v v v如果有边相连,则 F [ u ] [ v ] = w [ u ] [ v ] F[u][v]=w[u][v] F[u][v]=w[u][v],如果不相连,则 F [ u ] [ v ] = 0 x 3 f 3 f 3 f 3 f F[u][v]=0x3f3f3f3f F[u][v]=0x3f3f3f3f
2. 核心代码
for(int k = 1 ; k <= n ; k ++) {
for(int i = 1 ; i <= n ; i ++) {
for(int j = 1 ; j <= n ; j ++) {
if(F[i][j] > F[i][k] + F[k][j]) {
F[i][j] = F[i][k] + F[k][j];
}
}
}
}
3. 算法解释:
F [ i ] [ j ] F[i][j] F[i][j]得出的就是任意起点 i i i到任意终点 j j j的最短路径
- 动态规划以”途径点集大小”为阶段
- 决策需要枚举中转点,不妨考虑也以中转点集为阶段
- F [ k ] [ i ] [ j ] F[k][i][j] F[k][i][j]表示”可以经过标号 ≤ k ≤k ≤k的点中转时”从 i i i到 j j j的最短路
- F [ 0 ] [ i ] [ j ] = W [ i ] [ j ] F[0][i][j]=W[i][j] F[0][i][j]=W[i][j], W W W为前面定义的邻接矩阵
- F [ k ] [ i ] [ j ] F[k][i][j] F[k][i][j] = m i n min min{
F [ k − 1 ] [ i ] [ j ] F[k-1][i][j] F[k−1][i][j] , F [ k − 1 ] [ i ] [ k ] F[k-1][i][k] F[k−1][i][k] + F [ k − 1 ] [ k ] [ j ] F[k-1][k][j] F[k−1][k][j]}
- k k k这一维空间可以省略,变成 F [ i ] [ j ] F[i][j] F[i][j]
- 由于 k k k是 D P DP DP的阶段循环,所以 k k k循环必须要放在最外层
4. 使用 f l o y d floyd floyd输出最短路径:
F l o y d Floyd Floyd算法输出路径也是采用记录前驱点的方式。因为 f l o y d floyd floyd是计算任意两点间最短路径的算法, F [ i ] [ j ] F[i][j] F[i][j]记录从 i i i到 j j j的最短路径值。故我们定义 p r e [ i ] [ j ] pre[i][j] pre[i][j]为一个二维数组,记录从 i i i到 j j j的最短路径中, j j j的前驱点是哪一个,递归还原路径
- p r e [ i ] [ i ] pre[i][i] pre[i][i] 为 0,输入相连边时,重置相连边尾结点的前驱若有无向边: p r e [ a ] [ b ] = a pre[a][b]=a pre[a][b]=a, p r e [ b ] [ a ] = b ; pre[b][a]=b; pre[b][a]=b;
- 更新若 f l o y d floyd floyd最短路有更新,那么 p r e [ i ] [ j ] = p r e [ k ] [ j ] ; pre[i][j]=pre[k][j]; pre[i][j]=pre[k][j];
- 递归输出指两点 s s s, e e e的最短路,先输出起点 s s s,再将终点 e e e放入递归,输出 s + 1 − e s+1-e s+1−e的所有点。
核心代码:
void floyd() {
for (int k = 1 ; k <= n ; k ++) {
for (int i = 1 ; i <= n ; i ++) {
for (int j = 1 ; j <= n ; j ++) {
if (dp[i][k] + dp[k][j] < dp[i][j]) {
dp[i][j] = dp[i][k] + dp[k][j];
pre[i][j] = pre[k][j];
}
}
}
}
}
void print(int x) {
if (pre[s][x] == 0) return;
print(pre[s][x]);
printf(" %d", x);
}
2. d i j k s t r a dijkstra dijkstra
主要方法:
- 分成两组:已经确定最短路、尚未确定最短路
- 从第2组中选择路径长度最短的点放入第1组并扩展
- 本质是贪心,只能应用于正权图
- 普通的 D j k s t r a Djkstra Djkstra算法 O ( N 2 ) O(N^2) O(N2)
- 堆优化的 D i j k s t r a Dijkstra Dijkstra算法 O ( N l o g N ) − O ( M l o g N ) O(NlogN)-O(MlogN) O(NlogN)−O(MlogN)
引入概念——松弛操作:
- 原来用一根橡皮筋直接连接 a a a、 b b b两点,现在有一点k,使得 a − > k − > b a->k->b a−>k−>b比 a − > b a->b a−>b的距离更短,则把橡皮筋改为 a − > k − > b a->k->b a−>k−>b ,这样橡皮筋更加松弛。
- 代码实现: i f ( d i s [ b ] > d i s [ k ] + w [ k ] [ b ] ) d i s [ b ] = d i s [ k ] + w [ k ] [ b ] ; if(dis[b]>dis[k]+w[k][b])dis[b]=dis[k]+w[k][b]; if(dis[b]>dis[k]+w[k][b])dis[b]=dis[k]+w[k][b];
算法描述:
设起点为 s s s, d i s [ v ] dis[v] dis[v]表示从指定起点 s s s到 v v v的最短路径, p r e [ v ] pre[v] pre[v]为 v v v的前驱,用来输出路径
1.初始化
m e m s e t ( d i s , + ∞ ) memset(dis,+∞) memset(dis,+∞)
m e m s e t ( v i s , f a l s e ) memset(vis,false) memset(vis,false);
( i n t (int (int v = 1 ; v < = n ; v + + ) v = 1 ; v <= n ; v ++) v=1;v<=n;v++)
d i s [ v ] = w [ s ] [ v ] dis[v]=w[s][v] dis[v]=w[s][v];
d i s [ s ] = 0 dis[s]=0 dis[s]=0; p r e [ s ] = 0 pre[s]=0 pre[s]=0; v i s [ s ] = t r u e vis[s]=true vis[s]=true;
2. 松弛 n − 1 n-1 n−1次
- 在没有被访问过的点中找一个相邻顶点k,使得 d i s [ k ] dis[k] dis[k]是最小的;
- k k k标记为已确定的最短路 v i s [ k ] = t r u e vis[k]=true vis[k]=true;
- 用 f o r for for循环更新与k相连的每个未确定最短路径的顶点 v v v(所有未确定最短路的点都松弛更新)
3.算法结束
dis [ v ] [v] [v]为 s s s到 v v v的最短路距离; p r e [ v ] pre[v] pre[v]为 v v v的前驱结点,用来输出路径
让我们来看一组动画 (不动的动画)
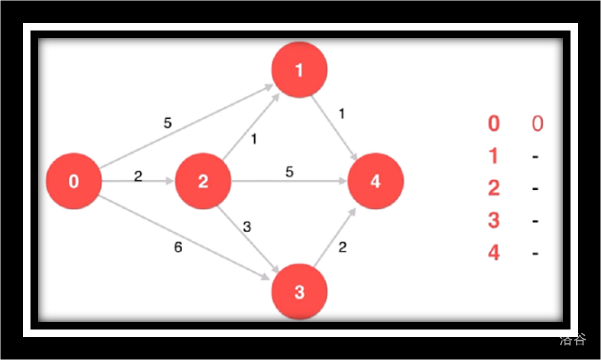
原始图
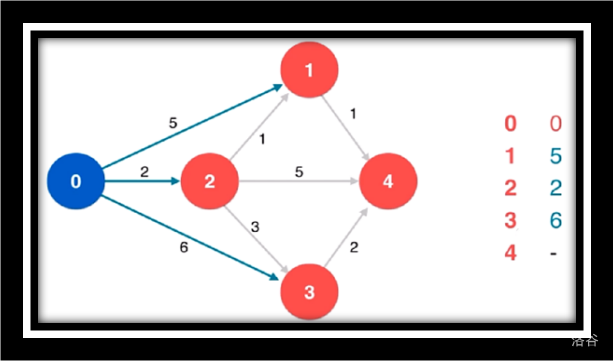
初始化
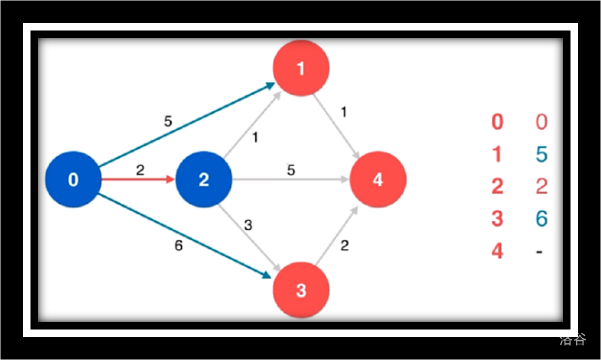
寻找源点相邻的最短路

松弛源点到1/4/3
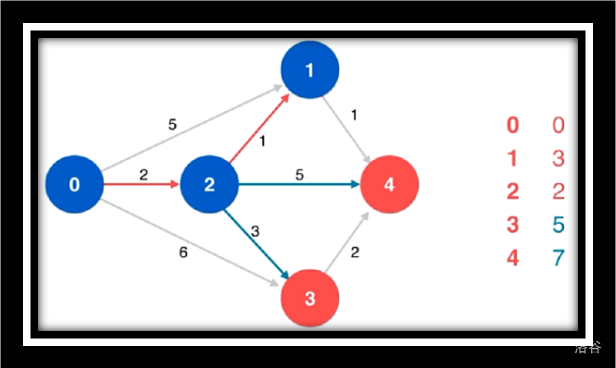
寻找源点到1/4/3的最短路

松弛源点到4
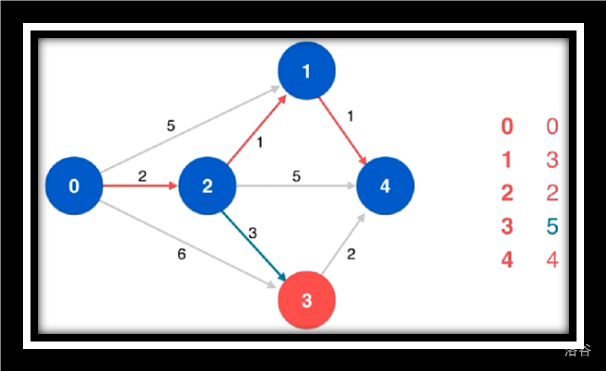
寻找源点到4的最短路由于点4没有相邻点故不作松弛操作

寻找剩余未访问点3松弛源点到4并未更改最短路
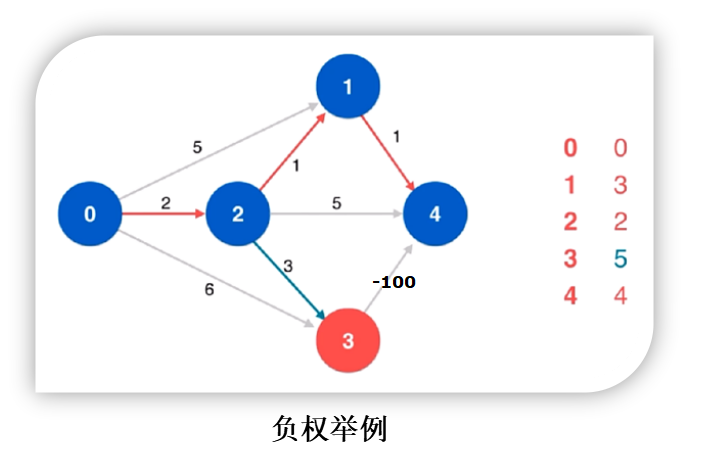
最后奉上本人的代码(优化后) :
struct edge{
int to , nxt , w;
}a[MAXN];
void add(int u , int v , int w) {
a[++ cnt].w = w;
a[cnt].to = v;
a[cnt].nxt = head[u];
head[u] = cnt;
}
struct node{
int id , w;
node(int iid , int ww) {
id = iid;
w = ww;
}
friend bool operator<(node x , node y) {
return x.w > y.w;
}
};
priority_queue<node> q;
void dijkstra() {
memset(dis , 0x3f , sizeof(dis));
dis[s] = 0;
q.push(node(s , 0));
while(!q.empty()) {
int u = q.top().id;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (int i = head[u] ; i ; i = a[i].nxt) {
int v = a[i].to , w = a[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push(node(v , dis[v]));
}
}
}
}
3. B e l l m a n − F o r d Bellman-Ford Bellman−Ford
- B e l l m a n − F o r d Bellman-Ford Bellman−Ford算法:对每条边执行更新,迭代 N − 1 N-1 N−1次
- 具体操作是对图进行最多 n − 1 n-1 n−1次松弛操作,每次操作对所有的边进行松弛,为什么是 n − 1 n-1 n−1次操作呢?这是因为我们输入的边不一定是按源点由近至远,万一是由远至近最坏情况就得 n − 1 n-1 n−1次
- 可以应用于负权图
- 预计时间复杂度: O ( n 2 ) O(n^2) O(n2)
非本人代码(不想打了):



想都不用想就知道有多慢
所以,我们引入了一个新的算法—— S P F A SPFA SPFA
4. S P F A ( s h o r t e s t SPFA(shortest SPFA(shortest p a s t past past f a s t fast fast a l g o r i t h m ) algorithm) algorithm)
- S P F A SPFA SPFA等于队列优化的 B e l l m a n − F o r d Bellman-Ford Bellman−Ford算法
- 本质上还是迭代——每更新一次就考虑入队
- 稀疏图上 O ( k N ) O(kN) O(kN),稠密图上退化到 O ( N 2 ) O(N^2) O(N2)
- 可以应用于有向负权图
- 算法实现:它采用了队列和松弛技术。先将源点加入队列。然后从队列中取出一个点(此时该点为源点),对该点的邻接点进行松弛,如果该邻接点松弛成功且不在队列中,则把该点加入队列。如此循环往复,直到队列为空,则求出了最短路径
- 判断有无负环:如果某个点进入队列的次数超过 N N N次则存在负环 ( 存在负环则无最短路径,如果有负环则会无限松弛,而一个带 n n n个点的图至多松弛 n − 1 n-1 n−1次)
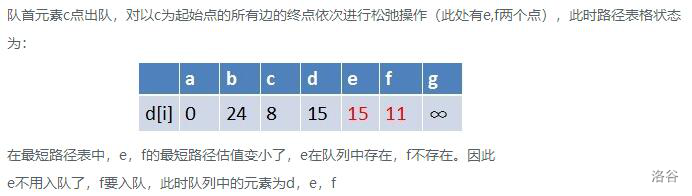





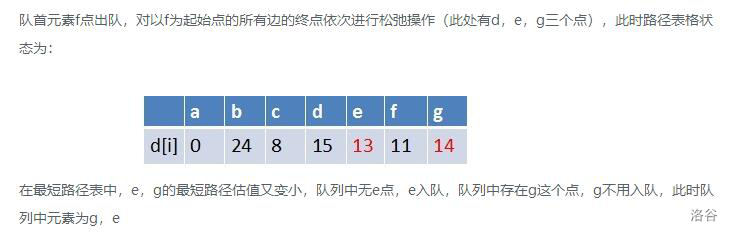



你理解了吗?
bool vis[MAXN];
struct edge{
int to , w , nxt;
}a[MAXN];
void add(int u , int v , int w) {
a[++ cnt].w = w;
a[cnt].to = v;
a[cnt].nxt = head[u];
head[u] = cnt;
}
struct node {
int id , w;
node(int iid , int ww) {
id = iid;
w = ww;
}
};
queue<node> q;
int SPFA() {
memset(dis , 0x3f, sizeof(dis));
dis[s] = 0;
q.push(node(s , 0));
while(!q.empty()) {
int u = q.front().id;
q.pop();
vis[u] = 0;
for (int i = head[u] ; i ; i = a[i].nxt) {
int v = a[i].to , w = a[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (!vis[v]) {
vis[v] = 1;
q.push(node(v , dis[v]));
}
}
}
}
return 1;
}
最小生成树
引入:树有这样一个定理: N N N个点用 N − 1 N-1 N−1条边连接成一个连通块,形成的图形只可能是树,叫做生成树!因此,一个有 N N N个点的连通图,边一定 ≥ N − 1 ≥N-1 ≥N−1条
概念:最小生成树 ( M i n i m u m (Minimum (Minimum S p a n n i n g Spanning Spanning T r e e s Trees Trees简称 M S T ) MST) MST)求带权无向图的一棵子树,包含 N N N个点, N − 1 N-1 N−1条边,边权之和最小
P r i m Prim Prim算法
算法思路:
- 以任意一个点为基准点
- 节点分为两组:
1)在 M S T MST MST上到基准点的路径已经确定的点
2)尚未在 M S T MST MST中与基准点相连的点 - 不断从第2组中选择与第1组距离最近的点加入第1组,类似于 D i j k s t r a Dijkstra Dijkstra,本质也是贪心, O ( N 2 ) O(N^2) O(N2)
算法描述:
总体思想:也使用“蓝白点”思想,白点代表已进入最小生成树的点,蓝点代表未进入最小生成树的点
以1为起点生成最小生成树, m i n [ v ] min[v] min[v]表示蓝点 v v v与白点相连的最小边权, M S T MST MST 表示最小生成树的权值之和
( a ) (a) (a)初始化: m i n [ v ] = ∞ ( v ≠ 1 ) min[v]=∞(v≠1) min[v]=∞(v=1); m i n [ 1 ] = 0 ; M S T = 0 ; min[1]=0;MST=0; min[1]=0;MST=0;
( b ) f o r ( i = 1 ; i < = n ; i + + ) (b)for(i=1;i<=n;i++) (b)for(i=1;i<=n;i++)
f o r for for寻找 m i n [ u ] min[u] min[u],最小的蓝点 u u u;
②将 u u u标记为白点;
③ M S T + = m i n [ u ] MST+=min[u] MST+=min[u];
④ f o r for for与白点 u u u相连的所有蓝点v(可暴力枚举,更好的是求 v e c t o r vector vector的 s i z e size size)
i f ( w [ u ] [ v ] < m i n [ v ] ) if(w[u][v]<min[v]) if(w[u][v]<min[v]) m i n [ v ] = w [ u ] [ v ] ; min[v]=w[u][v]; min[v]=w[u][v];
( c ) (c) (c)算法结束:MST即为最小生成树的权值之和
这次ppt的图片不是一个整体,太难盗图了,就直接上代码吧
void Prim() {
for (int i = 1 ; i <= n ; i ++) d[i] = 0x3f3f3f3f3f3f;
d[1] = 0;
q.push(node(1 , 0));
while(!q.empty()) {
int u = q.top().id;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (int i = head[u] ; i ; i = a[i].nxt) {
ll v = a[i].to;
ll w = a[i].w;
if (w < d[v] && !vis[v]) {
d[v] = w;
q.push(node(v , d[v]));
}
}
MST += d[u];
}
}
K r u s k a l Kruskal Kruskal算法
算法思路:
- 利用并查集,起初每个点各自构成一个集合
- 所有边按照边权从小到大排序,依次扫描
- 若当前扫描到的边连接两个不同的点集就合并
- 本质也是贪心, O ( M l o g N ) O(MlogN) O(MlogN)
- 与Prim算法相比,没有基准点,该算法是不断选择两个距离最近的集合进行合并的过程
算法描述:
( a ) (a) (a)初始化
①写出并查集三件套
②将边按权值大小排序
$(b)
① i f if if两个点的祖先不是同一个,将两个点合并,并累加权值;
②如果图已经联通,即 t o t = = n tot==n tot==n跳出
算法结束: M S T MST MST即为最小生成树的权值之和。
依旧很难盗图,无语
void kruscal() {
int tot = 0;
for (int i = 1 ; i <= m ; i ++) {
if (UnionSet(a[i].u , a[i].v)) {
MST += a[i].w;
tot ++;
if (tot == n) return;
}
}
}

智能推荐
matlab编程控制舵机,船舶航向控制器设计(MATLAB,附仿真程序)-程序员宅基地
文章浏览阅读1.1k次。船舶航向控制器设计(MATLAB,附仿真程序)(课题申报表,任务书,开题报告,中期检查表,外文翻译,论文15400字,仿真程序,答辩PPT)摘 要本文对反向递推(Backstepping)设计方法在非线性船舶航向控制器中的应用进行了研究。Backstepping设计方法是近几年兴起的一种基于Lyapunov稳定性理论的比较先进的非线性控制方法。因此,本文首先对目前常见的非线性控制方法进行了概述,简..._舵机模型matlab程序
营销系统优惠券模板设计_优惠劵表结构设置-程序员宅基地
文章浏览阅读819次。目录券模板基础信息定义优惠券类型优惠券门槛优惠券面值/折扣率,折扣金额上限有效期自定义使用限定使用时间限定可用商品限定可用门店限定券模板设计类似于商品SKU,定义了一个券模板后,发券操作可以基于同一个券模板实现发放同一种优惠券给多个不同的用户。券模板基础信息定义一张优惠券的基础信息,例如常规的名称,类型,面值等等。下面罗列一些有逻辑含义的字段。优惠券类型立减券: 无门槛或有门槛的满减券,达到使用门槛后可以立减指定金额。 折扣券:按商品价格减免指_优惠劵表结构设置
(深度学习快速入门)人工智能、机器学习和深度学习总体概述_人工智能与深度学习 简明教程-程序员宅基地
文章浏览阅读3k次,点赞15次,收藏67次。线性回归:线性回归假设输出变量是若干输入变量的线性组合,并根据这一关系求解线性组合中的最优系数。具体来说,线性回归的作用是求得一组参数wi,i=0.1.,,,.nwi,i=0.1.,,,.n,使预测输出可以表示为以这组参数为权重的实例属性的线性组合,引入常量x0=1x_{0}=1x0=1,线性回归试图学习的模型就是当实例只有一个属性时,输入和输出之间的关系就是二维平面上的一条直线;_人工智能与深度学习 简明教程
python读取串口速度跟不上_串口读取数据很慢,怎么解决-程序员宅基地
文章浏览阅读1.9k次。byte[] reb = new byte[0x400];reb = myCom.Read(0x400);就是这个读取串口数据的函数public byte[] Read(int NumBytes){byte[] lpBuffer = new byte[NumBytes];if (this.hComm == -1){throw new ApplicationException("串口没有打开");}..._python读取串口速度跟不上
浏览器工作原理详解_在线浏览原理图-程序员宅基地
文章浏览阅读3.9w次,点赞47次,收藏283次。这是一篇全面介绍 Webkit 和 Gecko 内部操作的入门文章,是以色列开发人员塔利·加希尔大量研究的成果。在过去的几年中,她查阅了所有公开发布的关于浏览器内部机制的数据,并花了很多时间来研读网络浏览器的源代码。她写道: 在 IE 占据 90%市场份额的年代,我们除了把浏览器当成一个“黑箱”,什么也做不了。但是现在,开放源代码的浏览器拥有了过半的市场份额,因此,是时候来揭开神秘的面纱,一探网_在线浏览原理图
机器学习-Anomaly Detection_根据f1值或者查准率与查全率的比例来选择ε-程序员宅基地
文章浏览阅读347次。Problem Motivation异常检测(Anomaly detection)是机器学习算法的一个常见应用。这种算法的一个有趣之处在于:它虽然主要用于非监督学习问题,但从某些角度看,它又类似于一些监督学习问题。假想你是一个飞机引擎制造商,当你生产的飞机引擎从生产线上流出时,你需要进行 QA(质量控制测试),而作为这个测试的一部分,你测量了飞机引擎的一些特征变量,比如引擎运转时产生的热量,..._根据f1值或者查准率与查全率的比例来选择ε
随便推点
疟原虫感染治疗癌症,灵感竟然来源于地图-程序员宅基地
文章浏览阅读909次。2月9日,央视一套《新闻30分》节目向全球宣布了陈小平科学研究团队的重大发明《疟原虫感染免疫疗法治疗晚期癌症》。“疟原虫可成为抗癌生力军”迅速占据新闻热搜榜,引发民众热议。为何引发疟疾带来痛苦的疟原虫可以抗癌?这背后有什么样的故事?1985年,在陈小平教授还在中山医科大学读研究生的时候,有一天老师讲疟疾的流行病学时,挂出一张地图,与下图很像——疟疾主要流行在非洲、赤道附近,可以理解为:蚊子多的...
PAT乙级C语言1005 继续(3n+1)思想_pat1005继续 c语言-程序员宅基地
文章浏览阅读95次。#include<stdio.h>void da(int*b,int r);int main(){ //输入数据 int n; scanf("%d",&n); int a[999]; for(int i=0;i<n;i++){ scanf("%d",&a[i]); } //记录重复的数的下标 int t=0; int b[999]; int p; for(int i=0;i<n;i++){ p=a[i]; for(int._pat1005继续 c语言
【啃书】《智能优化算法及其MATLAB实例》例5.1蚁群算法求解TSP问题_蚁群算法 约束优化 matlab-程序员宅基地
文章浏览阅读905次,点赞3次,收藏13次。文章目录问题描述仿真过程matlab源码问题描述仿真过程matlab源码%20201012lu注:该matlab代码成功在matlabR2019a运行%%%%%%%%%%%%%%%%%%%%蚁群算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clear all; %清除所有变量close all; _蚁群算法 约束优化 matlab
WPF页面切换之Page与Window_wpf window page-程序员宅基地
文章浏览阅读2.3k次。先从基础背景知识说起:一、Page与Window介绍1.应用程序GUI的所有内容都是包含在Window中的,想要显示东西?必须先创建一个Window或者一个Window的子类;2.Window下面可以直接写内容,写布局,但是这些内容和布局写完后只能是固定的、不可变的,这里是不可变是指Window的内容不会发生变化了,因为元素和布局是写死的了;3.在Window下面插入Frame作为容器,再用该Frame包含你的某个Page(***注意:所有的Page都需要容器包含,否则无法进行页面之间的跳转和导航!_wpf window page
C++抽象数据类型(ADT)表示和实现--链队列(Queue)_c++数据结构adt怎么写-程序员宅基地
文章浏览阅读1.5k次。先放上ADT的解释和预定义常量。抽象数据类型(ADT)是指一个数学模型以及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内部如何表示和实现无关,即不论其内部结构如何变化,只要它的数学特性不变,都不影响其外部的使用。以下是队列的抽象数据类型定义。_c++数据结构adt怎么写
空调采集网关让空调更智能,让节能更简单!_空调外接网关进行数据采集的方案-程序员宅基地
文章浏览阅读304次。钡铼技术作为全球行业领先技术水平的工业物联网硬件研发企业,拥有资深的工控物联网产品的研发能力以及专业的工业物联网技术研发团队,为大型园区、楼宇、医院、学校、工厂机房等多种场景提供中央空调集成通信解决方案,根据各大空调制造商运用的不同协议,钡铼技术研发的空调采集网关目前支持大金、日立、东芝、三菱电机、海信、海尔、松下、约克、三菱重工、美的、奥克斯、博世、LG、格力等多个领先空调品牌。空调控制系统由云服务器、空调采集网关、空调设备组成。2、据测算,在正确使用空调的前提下,制冷空调温度每提高1℃,可节电8%;_空调外接网关进行数据采集的方案